数据结构与算法-链表（上）

链表（Linked List）是一种数据结构。那么链表的用途有哪些呢? 经典的应用之一就是LRU缓存淘汰算法了。接下来我们带着这样一个思考：如何用链表实现LRU缓存淘汰算法。

缓存是一种提高数据读取性能的技术，在计算机硬件设计、软件开发中有者广泛的应用。如CPU缓存，数据库缓存、浏览器缓存。

缓存的空间大小有限，当缓存占满时，哪些数据应该被清理，哪些应该被保留，就需要缓存淘汰策略决定。常用的策略有 先进先出策略FIFO,最少使用策略LFU，最近最少使用策略LRU。

链表的存储结构

链表也是一种线性表，那么它与同为线性表的数组有什么区别呢？ 上图可看出链表与数组在存储结构的差异表现在是否占用连续的内存地址。数个组严格规定必须占用连续的内存地址，这使得数组有了随机访问的特性。而链表则不必占用连续的内存空间，使得链表得以有效利用内存碎片来分散的存储数据。不过，如此一来链表就不能随机访问了，对链表的访问需要从头结点开始依据链的指向一个一个的查找。

链表的结构很多，常见的有单链表、循环链表、双向链表

单链表

单链表的结构如上图，单链表只能只能从一个方向遍历，第一个节点叫做头节点。最后一个节点叫做尾结点。 每个节点包括一个数据域和一个指针域。数据域存储节点的数据，指针域存储的是下一个的节点的地址。尾指针的没有后继节点所以它的指针域为NUll。

链表支持数据的查找、插入和删除操作。

单链表的插入删除 插入操作的步骤：先将x的next指向c（x–>next=b–>next）,再将b的next指向x(b–>next=x)。 删除操作的步骤：直接将a的next指向c（a–>next = a–>next–>next）。

插入删除的时间复杂度为O(1)。查找的时间复杂度为O（n）。

循环链表

循环链表将链表的尾结点指向了头节点，以此构成了一个首尾相连的环状结构。

当要处理的数据具有环形结构的特点时就适合采用循环链表。比如约瑟夫问题。

双向链表

双向链表的节点增加了一个指针域，存储的是前驱节点的地址。因此双向链表可以从两个方向遍历。大大方便了查找前驱节点。

对于单链表来说插入、删除操作的本身的复杂度为O(1)，但实际操作中会先查找节点位置，而查找的时间复杂度为O(n)。所以实际的复杂度为O(n)。就拿删除来说，单向链表删除某个节点时需要知道它的前驱节点，但是因为前驱节点不能反向查找，就需要从头节点再遍历一次，极其浪费性能。但如果采用双向链表就可以轻松的得到前驱节点，因此时间复杂为O(1)。

这样看来双向链表比单向链表更加高效，这也就是为什么双向链表在实际的软件开发中应用更加广泛。

双向链表的节点增加了新的域存储前驱节点的地址，会增加存储空间的开销，这其实就是一种空间换时间的设计思想。

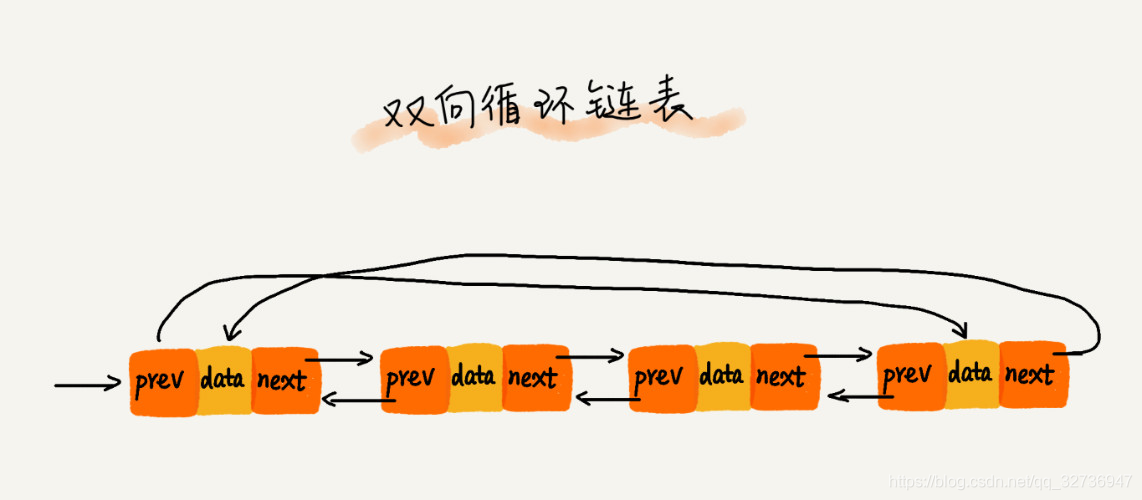
结合循环链表与双向链表我们可以得到双向循环链表

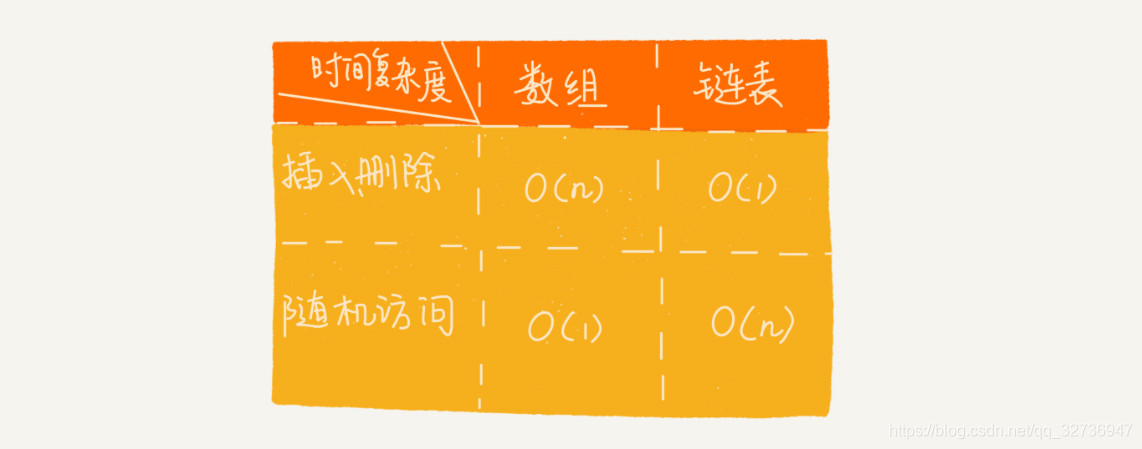
链表与数组的性能比较

LRU缓存淘汰策略实现

思路：维护一个有序单链表，越靠近链表尾部的节点是越早之前访问的，当访问一个新节点时从头结点开始遍历链表 1、如果该数据已经存在缓存链表中了，我们将其删除，然后插入到头节点。 2、如果不存在，分为两种情况： 此时缓存未满，将此节点插入到头部 此时缓存已满，将尾结点删除，然后将此节点插入到头部